Umor matematic
David Hilbert vorbind despre un elev al său spunea: "El a devenit poet. Pentru
matematică avea puţină imaginaţie".
Într-o noapte Blaise Pascal avea o groaznică durere de dinţi. A întrebuinţat
totul pentru potolirea durerilor, dar în zădar. Atunci s-a ocupat de studiul
cicloidei, descoperindu-i o serie de proprietăţi, ca să constate în final, că
durerea de dinţi a dispărut.
Marele matematician rus A. A. Marcov, fiind întrebat, ce este matematica, a
răspuns: "Matematica este ceea cu ce se ocupă Gauss, Cebâşev, Leapunov şi eu".
Vorbind despre feciorul său, David Hilbert spunea: "Aptitudinile matematice el
le-a moştenit de la mamă-sa, iar restul de la mine".
În timpul uneia dintre prelegerile sale, David Hilbet spunea:
– Fiecare om posedă un anumit orizont. Când se îngustează şi devine infinit de
mic, el se transformă în punct şi atunci omul zice: "Acesta este punctul meu de
vedere".
Odată Hilbert, împreună cu soţia sa, a organizat un dineu. După sosirea unui
oaspete, doamna Hilbert şi-a chemat soţul într-o parte şi i-a spus:
– David, du-te, te rog, şi-ţi schimbă cravata.
Hilbert dispăruse. Se scurseră o oră, dar el tot nu-şi făcea apariţia. Stăpâna
casei, îngrijorată, se porni în căutarea soţului. Privind şi în dormitor,
descoperi, spre mirarea ei că Hilbert dormea în pat. Trezindu-se, el şi-a
amintit că după ce şi-a scos cravata, continua, după inerţie, să se dezbrace
mai departe şi, după ce s-a îmbrăcat în pijama, s-a culcat în pat.
Odată Isaac Newton a vrut să-şi fiarbă un ou de găină, fără a întrerupe lucrul.
Îşi lua un cronometru pentru a fierbe oul numai în timp de trei minute. Era,
însă, preocupat de problema sa matematică, pe care încerca s-o rezolve în acel
moment. Când îşi aduse aminte, mare-i fu mirarea: a pus ceasul la fiert, iar în
mână ţinea oul ca să numere minutele.
Marele fizician Josiah Gibbs, fiind un om foarte retras, nu scotea, de obicei,
nici o vorbă la consiliile ştiinţifice ale universităţii unde el preda. La una
din şedinţele în cadrul căreia se discuta întrebarea cărui obiect trebuie de
rezervat mai mult spaţiu în noul program de studiu: matematicii sau limbilor
străine. Gibbs n-a răbdat, totuşi, şi a luat cuvântul:
– Matematica tot este limbaj, – a spus el.
Lui Albert Einstein îi plăceau foarte mult filmele lui Charles Chaplin, nutrind
o simpatie deosebită faţă de personajele create de acest cineast.
Într-o scrisoare adresată lui Charles Chaplin citim: "Filmul dumneavoastră
"Goana după aur" e pe înţelesul tuturor. Veţi ajunge numaidecât om mare.
Einstein".
Răspunsul a fost dat cu promptitudine: "M-aţi cucerit şi mai mult. "Teoria
relativităţii", pe care aţi elaborat-o, nu o înţelege nimeni, dar dumneavoastră
aţi devenit, totuşi, om mare. Chaplin".
Carl Gauss se distingea încă din şcoală prin agerimea minţii sale. Odată
învăţătorul său îi zise:
– Carl, aşi vrea să-ţi dau două întrebări. Dacă la prima o să răspunzi corect,
apoi la a doua poţi să nu mai răspunzi. Aşadar, câte ace are bradul şcolii
noastre, împodobit de Anul Nou?
– 65786 de ace, domnule învăţător, – a răspuns imediat Gauss.
– Bine, dar cum ai aflat acest lucru? – îl întrebă învăţătorul.
– Această întrebare de acum este cea de a doua, – remarcă cu promptitudine
elevul.
Printre numeroasele lecţii despre aplicaţiile matematicii, citite de către
Cebâşev, se remarcă şi prelegerea lui la Paris, dedicată teoriei matematicii în
confecţionarea îmbrăcămintei. La ea s-au prezentat cei mai buni croitori şi
modelieri, diferiţi experţi în ale eleganţei. Cebâşev şi-a început lecţia cu
renumita frază matematică:
– Admitem, pentru simplitate, că omul are corp de formă sferică.
După aceste cuvinte vorbele lui sunau în gol, deoarece publicul şocat a părăsit
sala.
Marele matematician american John von Neumann, a lucrat cândva în calitate de
consultant al specialiştilor din domeniul construirii navelor cosmice. Odată,
văzând scheletul unei rachete, von Neumann a întreabat pe colaboratorul ce-l
însoţea:
– Cine a construit racheta?
– Inginerii, – a fost răspunsul.
– Inginerii? – repetă von Neumann cu dispreţ, – păi eu am elaborat teoria
matematică a rachetelor. Luaţi respectiv, lucrarea mea, publicată în anul 1952,
şi veţi găsi în ea totul ce vă interesează.
Specialiştii au găsit lucrarea în cauză, au demontat construcţia rachetei
proiectate de ei (către acel moment erau cheltuite deja 10 000 000 de dolari)
şi au construit o rachetă nouă, urmărind cu stricteţe recomandările lui von
Neumann. Însă aceasta n-a fost destul, pentru a garanta succesul final, căci în
momentul apăsării butonului "Start" a răsunat o explozie asurzitoare şi racheta
s-a făcut ţăndări. Indignaţi, constructorii de rachete l-au chemat pe von
Neumann şi l-au întrebat:
– De ce, în pofida urmării cu stricteţe a recomandărilor dumneavoastră racheta
a explodat, totuşi, în momentul lansării ei.
– Ceia despre ce aţi vorbit se referă la aşa numita teorie a exploziei
puternice. Eu am elaborat într-o lucrare de a mea, publicaă în anul 1954. Veţi
găsi în ea totul ce vă interesează, – a răspuns von Neumann.
Niels Bohr avea de asupra uşii sale de la vilă bătută o potcoavă care,
chipurile, aduce conform unei credinţe populare, noroc.
– Poate oare un savant atât de remarcabil ca dumneavoastră să creadă, că
potcoava suspendată de asupra uşii într-adevăr aduce noroc? – întreabă unul din
vizitatorii săi.
– Nu, răspunse Bohr, – desigur că nu cred. Aceasta-i o veritabilă superstiţie.
Dar ştiţi se spune, că ea aduce noroc chiar şi celor care nu cred în aceasta.
Despre Jean d'Alembert se zice, că atunci când de fiecare dată demonstrează
studenţilor propria teoremă, spunea: "Şi acum, domnilor, vom trece la teorema
al cărei nume am onoarea să-l port".
Mare i-a fost mirarea unui filozof, când a aflat de la Bertrand Russell, că
dintr-o afirmaţie falsă poate fi dedusă oricare alta. El a întrebat:
– Dumnevoastră consideraţi, într-adevăr, că din afirmaţia 2 + 2 = 5,
urmează, că sunteţi papa de la Roma?
Russell dădu afirmativ din cap.
– Şi dumneavoastră puteţi demonstra acest lucru? – continuă să-şi exprime
îndoiala filozoful.
– Desigur! – a răspuns cu fermitate Russell şi-i expune demonstraţia în
cauză:
1. Presupunem, că 2 + 2 = 5;
2. Scădem din ambele părţi a egalităţii câte un doi: obţinem 2 = 3;
3. Schimbăm cu locurile partea stângă cu partea dreaptă: 3 = 2;
4. Scădem din ambele părţi câte o unitate: 2 = 1;
Papa de la Roma şi eu – împreună suntem doi. Deoarece 2 = 1, atunci papa
de la Roma şi eu suntem una şi aceeaşi persoană. Deci, eu sunt papa de la Roma.
Despre matematicianul francez Pierre de Maupertuis (de altfel, favoritul lui
Napoleon Bonaparte), se spune, că, după o masă copioasă şi bine stropită cu
băuturi, se aşează într-un fotoliu şi declară, căscând: "Acum aş vrea să rezolv
o problemă frumoasă, dar să nu fie prea dificilă!"
Un profesor foarte pedant obişnuia să spună: "... polinomul de gradul patru
ax4 + bx3 + cx2 +
dx + e,
unde
e nu-i neapărat să fie baza logaritmilor naturali" (dar poate şi să
fie).
Deducţia logică
Cică în coşul unui aerostat, luat de vânt şi ce pierdea din înălţime, se aflau
Sherlock Holmes şi doctorul Watson. Călătorii lui, în momentul când pierduseră
orice orientare, au zărit un om.
– Domnule, spuneţi-mi, vă rog, măcar aproximativ, unde ne aflăm? – întrebă
Holmes.
– De ce aproximativ, domnule? Vă pot spune precis. Vă aflaţi în coşul
aerostatului.
În acest moment o rafală de vânt zmunci aerostatul în sus.
– Să-l ia naiba de matematician, – bolmoji Holmes.
– Sunt uimit, ca de obicei, – spuse Watson, – cum de aţi aflat, că omul acesta
este un matematician?
– Păi, faptul este evident, – zice Holmes, – răspunsul lui este pe cât de
exact, pe atât şi de inutil.
Pseudomatematica
Fizicianul crede, că 60 se împarte fără rest la orice număr (mai mic decât 60,
desigur). El observă că 60 se împarte la 1, 2, 3, 4, 5, 6. Mai verifică câteva
numere, luate, după cum afirmă el la întâmplare, spre exemplu la 10, 15, 20,
30. Deoarece 60 se împarte şi la ele, fizicianul consideră că aceste date
experimentale sunt suficiente, pentru a demonstra, că 60 se împarte fără rest
la orice număr.
Inginerul bănuieşte, că toate numerele impare sunt şi prime (adică numerele
care se împart fără rest doar la 1 şi sine însuşi). În orice caz, demonstrează
el, 1 este număr prim, mai apoi urmează 3, 5 şi 7, toate fiind, fără îndoială,
numere prime. Dacă e să luăm pe 9, apoi ne lovim de un caz neplăcut: 9 nu e un
număr prim, dar 11 şi 13 sunt desigur prime.
– Revenind la numărul 9, – spune inginerul, – se poate conchide, că s-a produs
o eroare experimentală.
Noţiunea de evident
Un careva profesor de matematică, formulând în timpul lecţiei o teoremă, a
spus:
– Demonstraţia ei este evidentă.
– Dar de ce este evidentă? – întrebă un student cu acest prilej.
Profesorul se gândi niţel şi apoi ieşi din sală. Întorcându-se peste vre-o 20
de minute el anunţă:
– Teorema într-adevăr este evidentă.
După aceasta el îşi continuă imperturbabil prelegerea sa.
Cât priveşte cuvântul "evident" el poate fi interpretat în diferite modalităţi.
Iată doar câteva dintre ele.
1. Când profesorul A spune că o afirmaţie este evidentă, aceasta înseamnă, că-i
cunoscută auditoriului încă 2 săptămâni în urmă.
2. Când profesorul B spune că o afirmaţie este evidentă, atunci aceasta
înseamnă că, venind acasă, şi gândindu-vă asupra ei veţi înţelege, de ce ea
este evidentă.
3. Când profesorul C spune că o afirmaţie este evidentă, aceasta înseamnă că,
dedicându-vă întreaga viaţă, ce v-a mai rămas, meditaţiilor asupra sensului
celor spuse, posibil, veţi înţelege cândva, că afirmaţia, este justă.
Marele compozitor german Ludwig van Beethoven aşa şi nu a mai reuşit nici odată
să se familiarizeze cu toate operaţiile aritmetice. Înmulţirea şi împărţirea au
fost pentru el o taină nedescoperită. De exemplu, pentru a înmulţi 12 la 60,
genialul compozitor îl aduna pe 12 de 60 de ori la rând.
Este drept că, matematicienii nu s-au lăsat "îndatoraţi" faţă de arta muzicii.
Astfel, pentru marele matematician austriac Georg Vega, muzica era într-atât de
străină, încât el spunea:
– Nu există nici muzică bună, nici muzică rea. Există doar numai zgomot mult şi
zgomot puţin.
Gottfried Leibniz era credincios in felul său. Pentru el posibilitatea de a
scrie toate numerele cu ajutorul simbolurilor "0" şi "1", adică cu ajutorul
sistemului binar, constituie demonstraţia matematică a creaţiei lumii din
nimic, Dumnezeu fiind 1, iar nimicul – 0.
Suntem martorii pătrunderii vertiginoase a calculatoarelor electronice în cele
mai diverse domenii. Iată, de exemplu, la rezolvarea problemelor de ordin
"economic". Cică, un student, hotărând să aplice pe viu cunoştinţele acumulate,
intenţionă să alcătuiască un meniu optim, pentru a economisi câte ceva din
bursă. Zis şi făcut. După ce a introdus în calculator datele despre preţurile
şi conţinutul caloric ale bucatelor, servite la cantina studenţească, a cerut,
ca meniul să aibă norma calorică recomandată de medicină, iar preţul să fie
minim. Răspunsul a urmat neîntârziat: "18 pahare de cafea cu lapte pe zi".
Este interesant, că în matematica superioară există o relaţie cunoscută, ce
exprimă o legătură strânsă şi neaşteptată, totodată, între numerele
p, e, 1, 0 şi
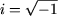 .
.
Este formula
eip + 1 = 0,
pe care a dedus-o Leonhard Euler. Ea, fiind o formulă cu multe sensuri, merită
atenţia nu numai a matematicienilor, ci şi a filozofilor şi reprezentanţilor
ştiinţelor naturale.
Matematicianul american Benjamin Peirce, luând cunoştinţă pentru prima dată de
această formulă, în pofida faptului că de la descoperirea ei trecuseră mai mult
de o sută de ani, a rămas foarte impresionat.
– Domnilor, – a spus el odată, adresându-se studenţilor, în momentul când
deduseseră relaţia pe tablă, – eu sunt convins, că formula scrisă este absolut
paradoxală. Noi nu suntem în stare s-o înţelegem, noi, însă, am demonstrat-o şi
de aceea considerăm, că ea este justă.
Un aspirant prea sacaitor l-a adus pe conducătorul său ştiinţific David Hilbert
într-o stare, încât acesta să-i spună: "Duceţi-vă şi elaboraţi construirea unui
poligon regulat cu 65 537 (= 2
16+1) de laturi". Aspirantul s-a retras, ca să revină după
20 de ani de activitate cu construcţia în cauză (actualmente ea se păstrează în
arhivele din Gottingen).
Odată matematicianul francez Joseph Louis Lagrange se afla la un concert.
Văzându-l foarte concentrat, cineva l-a întrebat, pentru ce îi place
muzica?
– Îmi place, – răspunde acesta, – fiindcă mă izolează. Ascult primele trei
măsuri; la a patra nu mai deosebesc nimic; mă las atunci furat de gândurile
mele; nimic nu mă mai întrerupe atunci; în felul acesta am rezolvat nu o
singură problemă dificilă.
Atunci când în anul 1884 studenţii Universităţii din Petersburg i-au dăruit
academicianului P. L. Cebâşev culegerea de lucrări, proaspăt ieşită de sub
tipar a cercului de matematică condus de el, Pafnutii Lvovici le-a spus:
– Scrieţi, scrieţi domnilor, dar nu uitaţi, că în timpurile noastre este mai
uşor şă găseşti trei cărţi decât un cititor.
Academia franceză a respins în mai multe rânduri lucrările lui Galois,
motivând, că ele sunt de neînţeles ... "din cauza dorinţei exagerate a
autorului de a se exprima prea concis". Mai târziu această instituţie a
apreciat, că lucrările lui Galios dispun ... de "o minunată claritate şi
precizie".
Matematicianul german Felix Klein, ce se ocupa în de aproape de chestiunile ce
ţin de instruirea matematică, a organizat înainte de Primul Război Mondial o
comisie internaţională pentru reorganizarea predării. Luând cunoştinţă de
gimnaziile nemţeşti, el a asistat şi la câteva lecţii. La una dintre ele,
atunci când s-a pomenit de Kopernik, Klein a întrebat: "Când a trăit
Kopernik?"
În continuare discuţia a decurs astfel:
Klein: Dacă nu ştiţi anii naşterii şi ai morţii, să-mi spuneţi, măcar, în ce
secol a trăit el?
Tăcere mormântală.
Klein: Spuneţi, a trăit înainte de era noastră sau nu?
Clasa (cu fermă convingere): Desigur, înainte de era noastră.
Klein remarcă: "Şcoala trebuia să obţină, ca elevii să răspundă la această
întrebare, cel puţin, fără a face uz de cuvântul "desigur"".
Matematicianul neamţ Moritz Pasch explica existenţa unui număr impunător de
oameni care nu înţeleg matematica, prin faptul că ... gândirea matematică, prin
însăşi esenţa ei, este opusă naturii omului.
George Berkeley afirma, că în calculul diferenţial se comit constant greşeli,
care apoi sunt corectate şi substituite cu alte greşeli de ordin opus.
Despre lucrările matematicianului Jordan se spunea, că dacă el ar fi avut
nevoie de patru mărimi analogice sau omogene (de exemplu
a,
b,
c,
d), el le-ar fi notat prin
a,
M3',
e2,
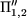
.
Matematicienii profesionişti sunt familiarizaţi cu numele celebrului
matematician al sec. XX Nicolas Bourbaki. De fapt, aceasta nu este numele unei
singure persoane, ci este pseudonimul unui grup de matematicieni, majoritatea
stabiliţi în Franţa şi care-şi respectă cu stricteţe anonimatul. Atingând
vârsta de 50 de ani, fiecare membru al acestui colectiv, indiferent de meritele
sale, este exclus automat din rândul celor activi. În pofida atmosferei de
taină, ce persistă în jurul biografiei lui N. Bourbaki, totuşi se cunoaşte
faptul că fondatorul acestui grup este matematicianul francez Jean
Dieudonne.
Cu prilejul primei sale vizite la Moskova, în anul 1966, J. Dieudonne
mărturisea: "Îl stimez foarte mult pe domnul Bourbaki, dar spre regret, nu-l
cunosc personal".
Însă cu ocazia editării în Uniunea Sovietică a "Elementelor matematicii"
(semnată N. Bourbaki) Jean Dieudonne a prezentat o procură autentificată, în care
N. Bourbaki încredinţa primirea onorarului pentru publicaţie "prietenului meu
J. Dieudonne".



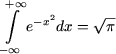 este evidentă ca "2
× 2 = 4".
este evidentă ca "2
× 2 = 4".





