Matematica vieții în toată splendoarea ei: Mathematica Learning Path for Primary and Secondary Educators

http://wolfram.com/xid/0fz3xp8d3e93ro

Out[6]=

You can open any or all of the subpanels to see numerical values, and you are free to animate many different variables at the same time if you like.

One way to think of Manipulate is as a way to interactively explore a large parameter space. You can move around that space at will, exploring interesting directions as they appear. As you will see in later sections, Manipulate has many features designed to make such exploration easier and more rewarding.

Symbolic Output and Step Sizes

The previous examples are graphical, and indeed the most common application for Manipulate is producing interactive graphics. But Manipulate is capable of making any Mathematica function interactive, not just graphical ones.

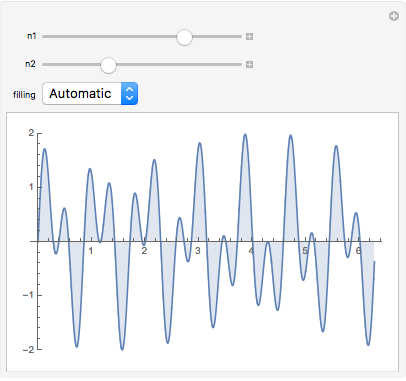
Often the first issue in examples involving symbolic, rather than graphical, output is that you want to deal with integers, rather than continuously variable real numbers. In Table the default step size is 1, so you naturally get integers, while in Manipulate the default is to allow continuous variation (which you could think of as a step size of zero). Compare these two examples, and note that Manipulate allows values in between those returned by Table.

In[7]:=

Out[7]=

In[8]:=

Out[8]=

Play Animation ▪

Functions involving algebraic manipulations, for example, often do nothing interesting when given noninteger parameter values. This Expand function never expands anything.

In[9]:=

Out[9]=

Play Animation ▪

Fortunately it is trivial to add an explicit step size of 1 to the Manipulate command, yielding exactly the same set of possible values in Manipulate as is returned by Table.

In[10]:=

Out[10]=

Play Animation ▪

With an explicit step size, the Expand example is much more interesting.

In[11]:=

Out[11]=

Play Animation ▪

The fact that only one value is displayed at a time allows you to create examples that go far beyond what would be practical in a Table command. An important property of Manipulate output is that there is no fixed panel size or arbitrary limit as to how large the output panel can grow.

In[12]:=

Out[12]=

Play Animation ▪

(In printed forms of this documentation, the slider is set fairly low to avoid wasting paper, but when moved all the way to the right, the output smoothly grows to cover many pages worth of vertical space.)

As with Table, if you use rational numbers for the minimum and step, you will get perfect rational numbers in the variable, not approximate real numbers. Here is an example that uses the formatting function Row to create a simple example of adding fractions.

In[13]:=

Out[13]=

Play Animation ▪

You can even use end points and step sizes that are symbolic expressions rather than just plain numbers.

In[14]:=

Out[14]=

Play Animation ▪

Types of Controls

Manipulate supports a wide range of alternate ways of specifying variables, which generate different kinds of controls for those variables. This includes checkboxes, popup menus, and others in addition to sliders.

The principle is that for each variable, you ask for a particular set of possible values, and Manipulate automatically chooses an appropriate type of control to make those values conveniently available. For a typical numerical Table-like iterator, a slider is the most convenient interface.

You might, on the other hand, want to specify a discrete list of possible values (numeric or symbolic) rather than a range. This is done with an iterator of the form

(Note the extra level of list compared to the range specification.) If you ask for a small number of separate values, you will get a row of buttons.

In[15]:=

Out[15]=

Play Animation ▪

If you ask for a larger number of discrete values, Manipulate will switch to using a popup menu.

In[16]:=

Out[16]=

Play Animation ▪

If you use the specific values True and False, you will get a checkbox.

In[17]:=

Out[17]=

Play Animation ▪

These choices are of course somewhat arbitrary, but they are designed to be convenient, and you can always override the automatic choice of control type using a ControlType option inserted into the variable specification. (The full list of possible control types is given in the documentation for Manipulate.)

For example, you can ask for a row of buttons even if the automatic behavior would have chosen a popup menu, using the option ControlType->SetterBar.

In[18]:=

Out[18]=

Play Animation ▪

Sliders can be used to scan through discrete symbolic values, not just through numerical ranges (and this allows you to animate through them as well). The option ControlType->Manipulator asks for the default control used by Manipulate, which is a slider plus an optional control panel with numerical value and animation controls (see the previous example). ControlType->Slider asks for a plain slider.

In[19]:=

Out[19]=

Play Animation ▪

It is even possible to use two different controls to adjust the value of the same variable. Here both a popup menu and a slider are connected to the value of the

variable. If the slider is used to select a value that does not appear in the popup menu, the popup will appear blank, but remains functional. When a value is chosen from the popup menu, the slider is moved to the corresponding position. Both controls can thus be used interchangeably to adjust the same value, and each one follows along when the other is being used.

In[20]:=

Out[20]=

Play Animation ▪

This is not an exhaustive list of the possible control types in Manipulate. See the Manipulate documentation for a more detailed listing. One of the most important control types, Locator, which allows you to place control points inside graphical output in a Manipulate, is discussed in "Locator"; Slider2D is discussed in the "2D Sliders" section.

Initial Values and Labels

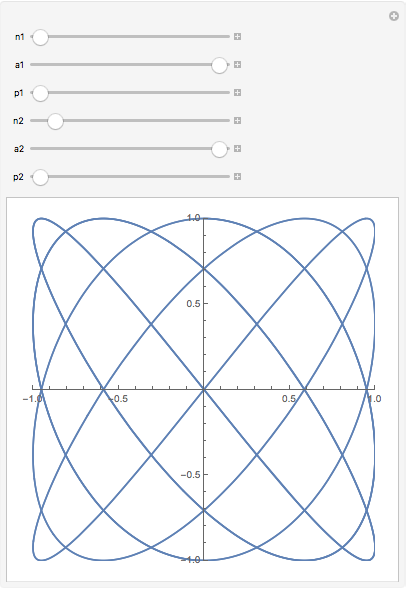
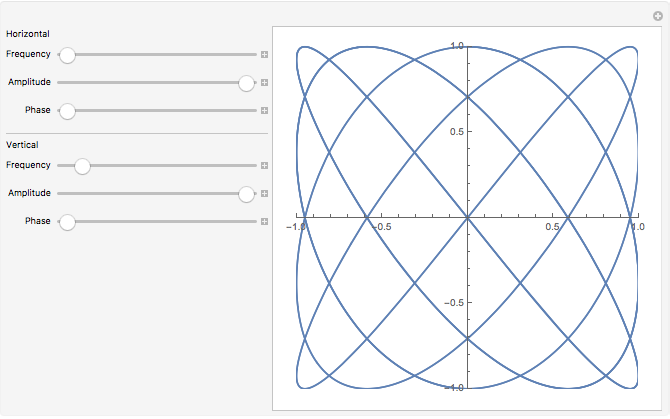
Here is a fun example for making Lissajous figures.

In[21]:=

Out[21]=

Play Animation ▪

Unfortunately you see nothing at first: until you move the

and

(amplitude) variables away from their initial values of zero, there is nothing to see. It would be convenient to set their initial value to something other than the default left-most value. This is done by using a variable specification of the form

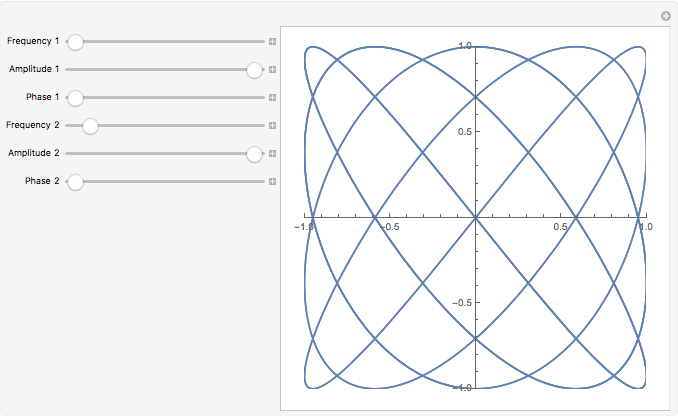
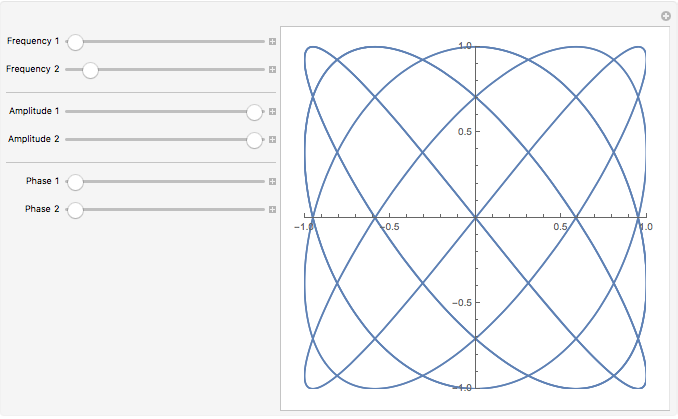
Here is the same example with both amplitudes set to 1 initially, and the default frequency values set to give a pleasing initial figure.

In[22]:=

Out[22]=

Play Animation ▪

It is fun to watch how one shape turns into another, and in this connection it is good to know about an unusual feature of sliders in Mathematica. If you hold down the Option key (Macintosh) or Alt key (Windows), the action of the slider will be slowed down by a factor of 20 relative to the movements of the mouse. In other words, when you drag the mouse left and right, the thumb will move only 1/20

as much as it normally would. If you move outside the area of the slider, the value will start moving slowly in that direction as long as the mouse remains clicked.

By holding down the Shift or Ctrl keys, or both, in addition to the Option/Alt key, you can slow the movement down by additional factors of 20 (one for each additional modifier key). With all three held down, it is possible to move the thumb by less than one part per million of its full range, which can be helpful in examples like this where beautiful patterns are hidden in very small ranges of parameter space.

(The option PerformanceGoal->"Quality" is used in this example to ensure that ParametricPlot draws smooth curves even when a slider is being moved: the need for this option is explained in more detail in "Advanced Manipulate Functionality".)

By default Manipulate uses the names of the variables to label each control. But you may want to provide longer, more descriptive labels, which can be done by using variable specifications of the form