Câtă matematică este în jurul nostru și cât de importantă este - merită să descoperim
sâmbătă, 29 martie 2014
miercuri, 26 martie 2014
Diagnosticul afectiunilor in functie de trasaturile fetei
In urma cu 5.000 de ani, practicantii medicinei chineze traditionale puteau “citi” starea de sanatate generala a unei persoane de pe chipul acesteia. Astfel, in functie de culoarea si textura pielii, de ridurile pe care le are, de mimica si reactiile din timpul unei discutii, medicii din Orient reuseau sa identifice 70% din problemele de sanatate ale pacientului doar privindu-l. Aceasta tehnica a fost folosita chiar si de calugarii taoisti, inzestrati cu harul vindecarii bolnavilor. Se spune chiar, ca prin observatie, medicul primeste cea mai mare cantitate de informatii, apreciata la 3 milioane biti/secunda.
Corpurile noastre sunt conectate prin linii de energie numite meridiane, care circula in sus si in jos. Iar desi practica citirii afectiunilor pe chip este destul de specifica, in mare, privindu-ne atent in oglinda putem descoperi simptomele unor posibile afectiuni. Fiecare parte anatomica a fetei reflecta starea de functionare a fiecarui organ. Potrivit principiilor medicinei traditionale chineze, obrajii sunt asociati cu plamanii, sprancenele cu ficatul, buzele cu sistemul digestiv, barbia cu vezica urinara, urechile si cearcanele cu rinichii s.a.m.d.
Pielea fetei mai este considerata si harta sanatatii, deoarece aceasta este foarte sensibila in fata schimbarilor care se petrec in corp. Aceasta este si explicatia pentru care tenul poate reflecta mult mai rapid transformarile interioare, comparativ cu alte zone anatomice.
Iata ce simptome pot indica aspectul si textura pielii
Paloare verzuie a fetei: disfunctii hepatice. Afectiunile hepatobiliare dau pielii culoarea galbena cu reflexe verzui.
Roseata permanenta a fetei: boli cardiovasculare sau hipertensiune arteriala.
Ingalbenirea tenului: functionare lenta a splinei/stomacului
Nuanta alba-bruna a tenului: semn de boala a rinichilor si cailor urinare.
Fata alba: boli de plamani si anemie.
Piele cu aspect uscat: tulburari endocrine, nervoase, gastrice, pulmonare si de circulatie.
Piele hiperhidratata: afectiuni renale, hepatobiliare si cardiovasculare.
Piele seboreica: tulburari endocrine, neuropsihice, intestinale si avitaminoze A si E.
Piele groasa, carnoasa, cu porii dilatati: tulburari hepatobiliare, metabolice si ale pancreasului.
Piele cuperozica: afectiuni nervoase, endocrine, digestive si de circulatie.
Pielea subtire, uscata, palida, cu aspect de pergament: anemii si tulburari endocrine.
Incretirea spatiului dintre sprancene: afectiuni ale sistemului limfatic, imunitate slabita.
Puncte rosii in jurul sprancenelor: instalarea gripei, sau a racelii.
Zona vascularizata a sprancenelor: sistem nervos hiperactiv, odihna insuficienta.
Pungi sub ochi: inflamatia rinichilor.
Nasul inrosit si santul orizontal pe lobul inferior al urechii: semnul tulburarilor cardiovasculare.
Urechile rosii: semne ale bolilor de rinichi si de circulatie.
Urechile uscate, cu aspect prafuit: afectiuni osoase.
Ridurile orizontale pe frunte: afectiuni ale sistemului nervos.
Ridurile verticale de la radacina nasului: consumul excesiv de produse animale.
Ridurile incrucisate: organismul este supus exceselor alimentare.
Buzele excesiv de rosii: afectiuni ale splinei si pancreasului.
Buzele uscate, uneori livide: afectiuni gastrice si colite.
Umflarea buzei superioare: boli de stomac.
Barbia umflata: boli de rinichi.
Alunite negre intre nas si buze: nivel crescut de toxine in corp.
Roseata permanenta a fetei: boli cardiovasculare sau hipertensiune arteriala.
Ingalbenirea tenului: functionare lenta a splinei/stomacului
Nuanta alba-bruna a tenului: semn de boala a rinichilor si cailor urinare.
Fata alba: boli de plamani si anemie.
Piele cu aspect uscat: tulburari endocrine, nervoase, gastrice, pulmonare si de circulatie.
Piele hiperhidratata: afectiuni renale, hepatobiliare si cardiovasculare.
Piele seboreica: tulburari endocrine, neuropsihice, intestinale si avitaminoze A si E.
Piele groasa, carnoasa, cu porii dilatati: tulburari hepatobiliare, metabolice si ale pancreasului.
Piele cuperozica: afectiuni nervoase, endocrine, digestive si de circulatie.
Pielea subtire, uscata, palida, cu aspect de pergament: anemii si tulburari endocrine.
Incretirea spatiului dintre sprancene: afectiuni ale sistemului limfatic, imunitate slabita.
Puncte rosii in jurul sprancenelor: instalarea gripei, sau a racelii.
Zona vascularizata a sprancenelor: sistem nervos hiperactiv, odihna insuficienta.
Pungi sub ochi: inflamatia rinichilor.
Nasul inrosit si santul orizontal pe lobul inferior al urechii: semnul tulburarilor cardiovasculare.
Urechile rosii: semne ale bolilor de rinichi si de circulatie.
Urechile uscate, cu aspect prafuit: afectiuni osoase.
Ridurile orizontale pe frunte: afectiuni ale sistemului nervos.
Ridurile verticale de la radacina nasului: consumul excesiv de produse animale.
Ridurile incrucisate: organismul este supus exceselor alimentare.
Buzele excesiv de rosii: afectiuni ale splinei si pancreasului.
Buzele uscate, uneori livide: afectiuni gastrice si colite.
Umflarea buzei superioare: boli de stomac.
Barbia umflata: boli de rinichi.
Alunite negre intre nas si buze: nivel crescut de toxine in corp.
De asemenea, se pare ca nici cariile nu apar tocmai intamplator. Medicii stomatologi au stabilit ca aparitia cariilor poate anunta anumite afectiuni. Astfel, cariile nu sunt numai boli ale dintilor, ci si semnele bolilor mai grave. Cariile aparute pe maxilarul superior la incisivi anunta bolile cardiovasculare, pe canini – afectiuni pulmonare si ale cailor respiratorii, la premolari – boli ale sistemului nervos si endocrin, iar pe molari – boli de stomac, hepatobiliare si endocrine. Cariile care se fac pe maxilarul inferior, indica afectiuni genitale daca apar pe incisivi, afectiuni renale – pe canini, boli ale intestinului gros si ale intestinului subtire – pe premolari si afectiuni hepatobiliare, endocrine si ale splinei – pe molari.
Avantajul principal al metodei chinezesti de observare a bolilor pe ten este ca multe boli pot fi prevenite prin adoptarea unui stil de viata mai sanatos si al unei alimentatii adecvate.
Si totusi cum arata chipul omului sanatos? Medicina chineza considera ca vitalitatea se manifesta prin urmatoarele aspecte:
- ten curat, lucios (discret), cu tesut subcutanat bine reprezentat (obraji carnosi)
- par lucios, rezistent, des
- retea densa a irisului si absenta petelor pe iris
- gura nu prea larga
- dinti regulati, sanatosi, fara carii
- forma rotunda a fetei, frunte inalta
marți, 25 martie 2014
BANCUL CU MAGARUL!
Stiti bancul cu magarul? Ei nu-i nimic ca vi-l spun eu: Un ţăran în târg. Vroia să-şi vândă magarul. Vine un cumpărător:
- Păi, bade, vinzi magarul ăsta?
- Îl vând!
- Dar ce are, e bolnav?
- N-are nimic!
- Atunci, poate nu mănâncă?
- Ba mănâncă!
- Nu trage la căruţă?
- Trage bine!
- Atunci de ce l-ai adus în târg?
- Ca să-l fac de râs.
- Păi, bade, vinzi magarul ăsta?
- Îl vând!
- Dar ce are, e bolnav?
- N-are nimic!
- Atunci, poate nu mănâncă?
- Ba mănâncă!
- Nu trage la căruţă?
- Trage bine!
- Atunci de ce l-ai adus în târg?
- Ca să-l fac de râs.

Cum sa se descurce la matematica?
Cum sa se descurce la matematica

Nota 10 la matematica
Cum il ajut pe copil la matematica? O intrebare pe care poate ti-ai pus-o adesea. Stapanirea tainelor matematicii este un obiectiv important pentru dezvoltarea ulterioara a copilului, in toate domeniile. Pentru cursurile de fizica sau de chimie copilul va avea nevoie de o baza solida de cunostiinte matematice; la fel si pentru a obtine note mari la admiterea in liceu sau facultate, lucruri care ii vor influenta fundamental evolutia in cariera. Iata cum il poti ajuta pe copil la matematica:
1. Asigura-te ca intelege concepte matematice
In caz contrar, matematica devine un exercitiu mental fara sens, care implica o simpla memorare a unor reguli ciudate sau actiuni de rutina. Pentru conceptele de baza foloseste-te de obiecte din viata de zi cu zi: spre exemplu, pentru a intelege adunarea pot aseza mai multe cuburi, unul peste altul, iar apoi vor numara cate cuburi sunt in turnulet.
2. Ajuta-i sa stapaneasca elementele de baza
Daca stapaneste o operatie, poate raspunde la o intrebare care implica acea operatie in mai putin de trei secunde. Pentru a ajunge in acest punct insa este necesara multa munca. Joaca-te de-a matematica impreuna cu el: pune-i intrebari din aritmetica si atunci cand nu poate raspunde lasa-l sa se foloseasca de obiecte in calcul.
3. Invata-l sa scrie corect cifrele
25% din greselile matematice facute de copii au la baza cifre si numere scrise neatent. Copilul poate invata cum sa scrie corect trecand cu pixul peste numere pe care tu le-ai scris deja cu creionul. De asemenea, este indicat sa se foloseasca pentru calcule caiete speciale de matematica ce ajuta la alinierea corecta a cifrelor.
4. Ajuta-l atunci cand are nevoie de tine!
Matematica este mereu construita pe bazele a ceea ce stii deja. Daca cineva are probleme cu intelegerea notiunii de procente, nu va putea stapani nici numerele rationale. Daca profesorul nu il poate ajuta pe copil, fii tu insuti un profesor sau apeleaza la un meditator potrivit.
5. Arata-i cum sa abordeze temele la matematica
Temele de casa ajuta la aprofundarea si consolidarea cunostiintelor dobandite la scoala. Invata-i sa inceapa fiecare tema citind lectia si exemplele rezolvate din manual. Sugereaza-le sa refaca singuri problemele rezolvate inainte de a le incepe pe cele din tema.
6. Incurajeaza-l sa faca mai mult decat tema de casa
Pentu stapanirea tainelor matematicii este necesar un exercitiu semnificativ. Daca obiceiul profesorului este de a lasa ca tema pentru acasa numai problemele cu numar impar, spre exemplu, incurajeaza-l pe cel mic sa faca si o parte din cele cu numar par. Cu cat mai mult timp este investit in exercitiu, cu atat mai repede va creste increderea in sine a copilului.
7. Explica-i cum sa citeasca enuntul problemei
Pentru a invata sa rezolvi probleme de matematica, trebuie sa rezolvi probleme de matematica! Spune-i copilului sa citeasca enuntul problemei de mai multe ori, eventual sa faca un desen / diagrama pentru a reprezenta problema. Fa intelegerea unei probleme mai usoara pentru ei, inlocuind numerele mari cu numere mai mici si mai abordabile.
8. Ajuta-l sa invete vocabularul matematicii
Nu va simti niciodata cu adevarat matematica si nici nu va putea invata concepte avansate fara sa inteleaga vocabularul matematic! Fii sigur ca cel mic poate defini termeni noi; daca nu, incearca sa creezi modele sau reprezentari simple pentru ca ei sa inteleaga mai usor.
9. Invata-i sa calculeze in minte
Matematica mentala este o modalitate foarte importanta de a rezolva probleme, chiar si in situatii de zi cu zi. Copiii ar trbeui incurajati cat mai mult sa isi foloseasca mintea si nu calculatorul sau hartia.
10. Aseaza matematica in viata cotidiana a copilului
Matematica va deveni mai semnificativa atunci cand copilul tau va vedea cat de importanta este in numeroase situatii din existenta sa. Incurajeaza-i sa foloseasca matematica intr-un mod practic. spre exemplu, lasa-i sa faca cumparaturi si sa primeasca restul, roaga-i sa planteze flori in curte la o anumita distanta una de alta etc.
Misterul patratului lipsa
Misterul pătratului lipsă
Cele două triunghiuri din figură sunt congruente, în consecinţă ar
trebui să aibă aceeaşi arie. Cu toate acestea, unul dintre triunghiuri
are aria mai mare cu o unitate decât celălalt. Cum poate fi posibil?
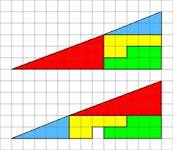
Explicaţia acestui aparent paradox constă în aceea că nici unul dintre cele două “triunghiuri” dreptunghice , avand o cateta de 5 si cealaltă catetă 13 , nu este cu adevărat un triunghi deoarece ipotenuza este curbată (de fapt frântă), chiar dacă la prima vedere nu se poate afirma acest lucru.
Un triunghi având dimensiunile precizate, nu poate fi de fapt alcătuit din formele geometrice respective.
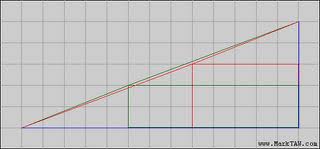
Ipotenuzele celor două triunghiuri mici (cel albastru şi cel roşu) nu au ambele aceeaşi înclinare. Cele două triunghiuri par a fi asemenea, dar dacă calculăm panta ipotenuzei triunghiului albastru obţinem: 5:2(=2.5:1) , în timp ce pentru triunghiul roşu raportul este 8:3(=2.(6):1) ceea ce demonstrează că ipotenuza triunghiului mare este de fapt o linie frântă.
Deoarece raporturile calculate sunt aproape egale, diferenţa este greu de sesizat cu ochiul liber cu atât mai mult cu cât marginile figurilor sunt destul de groase.
Dacă realizăm o imagine exactă a celor două triungiuri, eventual suprapuse, vom vedea că cele doua “ipotenuze” frânte formează un paralelogram al cărei arie este 1, adică exact diferenţa de arie dintre cele două triunghiuri.
Obţinem deci

Explicaţia acestui aparent paradox constă în aceea că nici unul dintre cele două “triunghiuri” dreptunghice , avand o cateta de 5 si cealaltă catetă 13 , nu este cu adevărat un triunghi deoarece ipotenuza este curbată (de fapt frântă), chiar dacă la prima vedere nu se poate afirma acest lucru.
Un triunghi având dimensiunile precizate, nu poate fi de fapt alcătuit din formele geometrice respective.
Ipotenuzele celor două triunghiuri mici (cel albastru şi cel roşu) nu au ambele aceeaşi înclinare. Cele două triunghiuri par a fi asemenea, dar dacă calculăm panta ipotenuzei triunghiului albastru obţinem: 5:2(=2.5:1) , în timp ce pentru triunghiul roşu raportul este 8:3(=2.(6):1) ceea ce demonstrează că ipotenuza triunghiului mare este de fapt o linie frântă.
Deoarece raporturile calculate sunt aproape egale, diferenţa este greu de sesizat cu ochiul liber cu atât mai mult cu cât marginile figurilor sunt destul de groase.
Dacă realizăm o imagine exactă a celor două triungiuri, eventual suprapuse, vom vedea că cele doua “ipotenuze” frânte formează un paralelogram al cărei arie este 1, adică exact diferenţa de arie dintre cele două triunghiuri.

Probleme distractive
- O populaţie de bacterii se dublează la fiecare oră a zilei şi se înjumătăţeşte la fiecare oră din noapte. Se consideră ziua de 13 ore şi noaptea de 11 ore. De câte ori va creşte populaţia de bacterii după 7 zile?
- O maşină pleacă la ora 12 din P cu viteza de 90 km/h. La ce oră îl va ajunge pe un biciclist plecat la ora 7 dimineaţa cu viteza de 15 km/h?
- O găină şi jumătate face un ou şi jumătate înt-o zi şi jumătate. Câte ouă fac 3 găini în 3 zile?
- De câte ori pe zi sunt limbile ceasului perpendiculare pe durata unei zile?
- Am tăiat o prăjitură în 4 părţi de-a lungul diagonalelor. Am mâncat o parte. Se cântăresc celelalte părţi şi rezultatele sunt: 120 g, 200 g şi 300 g. Care a fost greutatea părţii pe care am mâncat-o?
- Patru borcane cilindrice au fost dispuse pe fundul circular al unei cratiţe, cât mai aproape posibil, ca în desen. Dacă raza bazei unui borcan este 1, cât este raza bazei cratiţei?
- Două cercuri au centrle pe aceeaşi diagonală a unui pătrat. Ele sunt tangente între ele şi de asemenea, cu câte două laturi ale pătratului. Dacă lungimea laturii pătratului este de 1 cm, care este suma lungimilor razelor celor 2 cercuri?
- Formatul unei coli de hârtie numit A4, este un dreptunghi având raportul acelaşi cu raportul dreptunghiului obţinut prin tăierea colii A4 în două prin mijlocul lungimii. Să se calculeze .
- Intr-un depou se făcea manevra cu două locomotive; când acestea se aflau le distanţa de 30 m , pe aceeaşi linie ferată, mergând una spre alta cu viteza de 4,5 km/h fiecare, o muscă aflată pe tamponul din faţă al unei locomotive a pornit în zbor cu viteza de 6 km/h spre cealaltă locomotivă până la tamponul ei frontal, apoi imediat s-a întors la tamponul primei locomotive şi a tot făcut asemenea curse până când locomotivele atingându-se au strivit sărmana muscă… Ce distanţă a prcurs musca în această promenadă a ei?
- După 24 de ore populaţia de bacterii creşte de 4 ori deoarece se dublează pentru fiecare oră în plus dintre cele două cu care ziua este mai mare decât noaptea. După 7 zile populaţia se va mări de ori adică de ori.
- In cele 5 ore care s-au scurs de la ora 7 la ora 12, biciclistul a parcurs km. Peste încă o oră el va fi parcurs 90 de km, distanţă egală cu cea parcursă de maşină într-o singură oră. Deci după o oră de la pornirea automobilului, acesta se va afla lângă biciclist. Acest lucru se va petrece la ora 13.
- Există 3 mărimi: numărul de ouă, numărul de găini, şi numărul de zile. Prima mărime este direct proporţională atât cu a doua cât şi cu a treia. Aplicând de două ori regula de 3 simplă obţinem: O gaină şi jumătate face 3 ouă in 3 zile, în timp ce 3 găini vor face 6 ouă în 3 zile. Răspunsul corect este 6 ouă.
- De-a lungul unei ore oricare ar fi ea, minutarul este situat perpendicular faţă de orar de exact 2 ori. Cum într-o zi sunt 24 de ore, pe durata unei zile întregi, cele două ace ale ceasului vor fi perpendiculare de 48 de ori
- Considerăm numerele date ca fiind ariile părţilor de prăjitură. Astfel avem:
Obţinem deci
6. Unind centrele cercurilor mici se obţine pătrat cu latura , deci
diagonala este de , de unde diametrul cratiţei este . Rezultă că raza
cratiţei este de .Observaţie: Având în vedere caracterul distractiv al
problemelor/ întâlnirii nu s-a cerut demontrarea faptului că prin unirea
centrelor celor 4 cercuri obţinem un pătrat şi nici că centrul cercului
mare, centrul cercului mic şi punctul de tangenţă dintre cercul mic şi
cercul mare sunt coliniare pentru oricare dintre cercurile mici.
7. Distanţa de la centrul unui cerc la cel mai apropiat colţ este , respectiv . Diagonala pătratului mare se poate exprima astfel:
Cunoscând viteza de zbor a muştei, , distanţa totală pe care ar a prcurs-o în acea promenadă este:
7. Distanţa de la centrul unui cerc la cel mai apropiat colţ este , respectiv . Diagonala pătratului mare se poate exprima astfel:
- Mai întâi aflăm timpul necesar ca cele două locomotive să se întâlnească, ţinând cont că vitezele lor se adună atunci când se deplasează in sens contrar. Aceasta se va realiza împărţind distanţa la viteză:
Planificare Calendaristică Anuală Orientativă
Planificare
Calendaristică Anuală Orientativă
Unitatea de învăţare
|
Competenţe specifice
|
Conţinuturi
|
Nr.
ore
|
Săptă-mîna
|
Grupuri
|
1.
Recunoasterea structurilor algebrice, a mulŃimilor
de
numere, de polinoame si de matrice
2.1
Identificarea unei structuri algebrice, prin
verificarea
proprietătilor acesteia
2.2
Determinarea si verificarea proprietătilor
unei
structuri
3.1.
Verificarea faptului că o functie dată este
morfism sau izomorfism
|
Recapitulare
|
S1
|
|
Legi de compoziţie. Definiţie şi exemple
|
||||
Tabla de lege a unei operaţii. Adunarea şi înmulţirea
claselor de resturi modulo „n”
|
||||
Parte stabilă
|
S2
|
|||
Proprietăţi ale
legilor de compoziţie: comutativitatea şi asociativitatea
|
||||
Proprietăţi ale legilor de compozitie:
element neutru şi elemente simetrizabile
|
||||
Noţiunea de grup. Exemple
|
S3
|
|||
Exerciţii
|
||||
Exemple de grupuri: Grupuri de permutări
|
||||
Exemple de grupuri: Grupul claselor de resturi
modulo n
|
S4
|
|||
Exemple de grupuri: Grupuri de matrice
|
||||
Morfisme de grupuri
|
||||
Aplicaţii
|
S5
|
|||
Evaluare
|
||||
Inele şi corpuri
|
1.
Recunoasterea structurilor algebrice, a multimilor
de
numere, de polinoame si de matrice
2.1
Identificarea unei structuri algebrice, prin
verificarea
proprietătilor acesteia
2.2
Determinarea si verificarea proprietătilor
unei
structuri
3.1.
Verificarea faptului că o functie dată este
morfism sau izomorfism
|
Noţiunea de inel. Inele numerice
|
||
Reguli de calcul întrun inel
|
S6
|
|||
Exemple de inele: inele de matrice, inele de
funcţii reale
|
||||
Exerciţii
|
||||
Noţiunea de corp. Corpuri numerice
|
S7
|
|||
Corpul (Zp,+,*)
|
||||
Exerciţii
|
||||
Evaluare
|
S8
|
|||
Inele de polinoame
|
3.2.
Aplicarea unor algoritmi în calculul polinomial
sau
în rezolvarea ecuatiilor algebrice
4.
Explicarea modului în care sunt utilizate, în
calcule
specifice, proprietătile operatiilor
unei
structuri algebrice
5.
1. Utilizarea structurilor algebrice în rezolvarea
de
probleme practice
5.2.
Determinarea unor polinoame sau ecuatii
algebrice
care îndeplinesc conditii date
6.1
Exprimarea unor probleme practice, folosind
structuri
algebrice sau calcul polinomial
6.2
Aplicarea, prin analogie, în calcule cu
polinoame, a metodelor de lucru dinaritmetica numerelor
|
Forma algebrică
a unui polinom. Gradul unui polinom. Egalitatea a doua polinoame
|
||
Operaţii cu
polinoame: adunarea şi înmulţirea.
|
||||
Teorema împărţirii
cu rest a polinoamelor. Algoritmul de împărţire a două polinoame
|
S9
|
|||
Împărţirea cu
X-a. Schema lui Horner.
|
||||
Exerciţii
|
||||
Teza
|
S10
|
|||
Teza
|
||||
Teza
|
||||
Divizibilitatea
polinoamelor. Cmmdc si cmmmc a două polinoame
|
S11
|
|||
Rădăcina unui
polinom. Teorema lui Bezout
|
||||
Exerciţii
|
||||
Exerciţii
|
S12
|
|||
Descompunera unui polinom în factori
ireductibili
|
||||
Exerciţii
|
||||
Exerciţii
|
S13
|
|||
Relaţiile lui Viete pentru polinoame de grad
cel mult 4
|
||||
Exerciţii
|
S14
|
|||
Exerciţii
|
||||
Exerciţii
|
||||
Evaluare
|
||||
Ecuaţii algebrice cu coeficientii în Z
|
S15
|
|||
Ecuaţii algebrice cu coeficientii în Q
|
||||
Ecuaţii algebrice cu coeficienţii reali
|
||||
Ecuaţii algebrice cu coeficienţii complecşi
|
S16
|
|||
Ecuaţii bipătrate
|
||||
Ecuaţii binome
|
||||
Ecuaţii reciproce
|
S17
|
|||
Exerciţii
|
||||
Evaluare
|
||||
Primitive
|
1.
Identificarea legăturilor dintre o functie
continuă si
derivata sau primitiva acesteia
2.
Stabilirea unor proprietăti ale calculului
integral, prin analogie cu proprietăti alecalculului diferential
|
Probleme care conduc la noţiunea de
integrală
|
S18
|
|
Primitivele unei funcţii; integrala
nedefinită a unei funcţii continue
|
||||
Primitive uzuale
|
||||
Proprietăţi ale integralei nedefinite:
liniaritatea, adititvitatea în raport cu intervalul
|
S19
|
|||
Metode de calcul a primitivelor: formula de
schimbare de variabilă
|
||||
Metode de calcul a primitivelor: formula de
schimbare de variabilă
|
||||
Metode de calcul a primitivelor: integrarea
prin părţi
|
S20
|
|||
Metode de calcul a primitivelor: integrarea
prin părţi
|
||||
Evaluare
|
||||
Definirea integralei Riemann cu formula
Leibnitz-Newton
|
S21
|
|||
Prioprietăţi ale integralei definite;
liniaritatea, aditivitatea în raport cu intervalul
|
||||
Proprietatea de monotonie, de medie, modulul
integralei
|
||||
Integrala definită
|
3.
Utilizarea algoritmilor pentru calcularea
unor
integrale definite
4.
Explicarea optiunilor de calcul al integralelor
definite,
în scopul optimizării solutiilor
5.
Determinarea ariei unei suprafete plane si
a
volumului unui corp, folosind calculul
integral,
si
compararea rezultatelor cu
cele
obtinute
prin aplicarea unor formule
cunoscute
din geometrie
6. Aplicarea calculului diferential
sau integral în probleme practice
|
Exerciţii
|
S22
|
|
Metode de calcul a integralei definite:
integrarea prin părţi
|
||||
Metode de calcul a integralei definite:
integrarea prin schimbare de variabilă
|
||||
Aplicaţii
|
S23
|
|||
Aplicaţii
|
||||
Aplicaţii
|
||||
Calculul integralelor funcţiilor raţionale
prin descompunerea în factori
|
S24
|
|||
Aplicaţii
|
||||
Aplicaţii ale integralei definite: aria unei
suprafeţe plane, volumul corpului de rotaţie
|
||||
Aplicaţii
|
S25
|
|||
Aplicaţii
|
||||
Evaluare
|
||||
Teza
|
Recapitulare
|
S27
|
||
Lucrare semestrială
|
||||
Discutarea tezelor
|
||||
Recapitulare pentru bacalaureat
|
Algebră liniară
|
S28
|
||
Algebră liniră
|
||||
Limite de funcţii
|
||||
Funcţii continue
|
S29
|
|||
Funcţii derivabile
|
||||
Integrale nedefinite
|
||||
Integrale definite
|
S30
|
|||
Structuri algebrice
|
||||
Inele de polinoame
|
Unitatea
de învăţare
|
Competenţe specifice
|
Conţinuturi
|
Nr.
ore
|
Săptă-mâna
|
Planificarea orelor de geometrie- trigonometrie
|
||||
Vectori
in plan
|
Introducere in geometrie
|
S9
|
||
Segment orientat, relatie de echipolenta .
Vectori liberi
|
||||
Adunarea vectorilor in plan. Proprietati
|
S11
|
|||
Inmultirea vectorilor cu un scalar.
Proprietati
|
||||
Aplicatii
|
S12
|
|||
Conditia de coliniaritate a doi vectori
|
||||
Aplicatii
|
S13
|
|||
Descompunerea unui vector dupa doua directii
date. Baza. Coordonatele unui vector liber in plan.
|
||||
Aplicatii
|
S14
|
|||
Evaluare
|
||||
Aplicatii
|
S15
|
|||
Punctul care imparte un segment intr-un
raport dat
|
||||
Aplicatii
|
S16
|
|||
Coliniaritate, concurenta, paralelism
|
Vectorul de pozitie al unui punct in plan
|
|||
Vectorul de pozitie al mijlocului unui
segment, vectorul de pozitie al punctului care imparte un segment intrun
raport dat
|
S17
|
|||
Aplicatii
|
||||
Probleme de coliniaritate: Teorema lui
Thales
|
S18
|
|||
Probleme de concurenta: concurenta
medianelor:vectorul de pozitie al
centrului de greutate
|
||||
Concurenta bisectoarelor. Vectorul de
pozitie al centrului cercului inscris
|
S19
|
|||
Concurenta inaltimilor. Relatia lui
Sylvester
|
||||
Aplicatii (consecinte ale relatiei lui
Sylvester)
|
S20
|
|||
Teorema lui Menelau. Teorema lui Ceva.
|
||||
Aplicatii
|
S21
|
|||
Aplicatii
|
||||
Evaluare
|
S22
|
|||
Cercul trigonometric; definitie
|
||||
Transformarea din grade in radiani. Functa
de acoperire universala
|
S23
|
|||
Definirea functiilor trigonometrice pe [0 2pi]
|
||||
Definirea
functuiilor trigonometrice pe R; proprietatea de periodicitate
|
S24
|
|||
Formule de
reducere la primul cadran
|
||||
Relatii intre
functiile trigonometrice ale aceluiasi unghi
|
S25
|
|||
Trigonometrie
|
Aplicatii
|
|||
Aplicatii
|
S27
|
|||
Formule
trigonometrice ale sumei si diferentei de unghiuri
|
||||
Foemue pentru
argumentul dublu
|
S28
|
|||
Aplicatii
|
||||
Transformarea
sumelor in produs si produselor in sume
|
S29
|
|||
Aplicatii
|
||||
Teza
|
S30
|
|||
Teza
|
||||
Aplicatii ale trigonometriei in geometrie
|
Produsul scalar a doi vectori. Definitie.
Proprietati
|
S31
|
||
Aplicatii ale produsului scalar: teorema
cosinusului, conditia de perpendicularitate
|
||||
Aplicatii
|
S32
|
|||
Teorema sinusurilor. Rezolvarea triunghiului
oarecare
|
||||
Aplicatii
|
S33
|
|||
Formule pentru aria unui triunghi
|
||||
Aplicatii
|
S34
|
|||
Calculul razei si lungimilor unor segmente
importante
|
||||
Aplicatii
|
S35
|
|||
Aplicatii
|
S35
|
|||
Recapitulare finala
|
S36
|
|||
Recapitulare finala
|
||||
Abonați-vă la:
Comentarii (Atom)





