Misterul pătratului lipsă
Cele două triunghiuri din figură sunt congruente, în consecinţă ar
trebui să aibă aceeaşi arie. Cu toate acestea, unul dintre triunghiuri
are aria mai mare cu o unitate decât celălalt. Cum poate fi posibil?
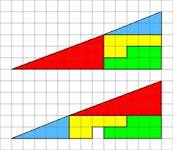
Explicaţia acestui aparent paradox constă în aceea că nici unul dintre cele două “triunghiuri” dreptunghice , avand o cateta de 5 si cealaltă catetă 13 , nu este cu adevărat un triunghi deoarece ipotenuza este curbată (de fapt frântă), chiar dacă la prima vedere nu se poate afirma acest lucru.
Un triunghi având dimensiunile precizate, nu poate fi de fapt alcătuit din formele geometrice respective.
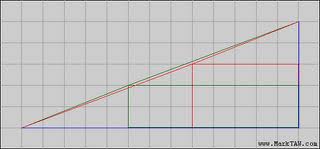
Ipotenuzele celor două triunghiuri mici (cel albastru şi cel roşu) nu au ambele aceeaşi înclinare. Cele două triunghiuri par a fi asemenea, dar dacă calculăm panta ipotenuzei triunghiului albastru obţinem: 5:2(=2.5:1) , în timp ce pentru triunghiul roşu raportul este 8:3(=2.(6):1) ceea ce demonstrează că ipotenuza triunghiului mare este de fapt o linie frântă.
Deoarece raporturile calculate sunt aproape egale, diferenţa este greu de sesizat cu ochiul liber cu atât mai mult cu cât marginile figurilor sunt destul de groase.
Dacă realizăm o imagine exactă a celor două triungiuri, eventual suprapuse, vom vedea că cele doua “ipotenuze” frânte formează un paralelogram al cărei arie este 1, adică exact diferenţa de arie dintre cele două triunghiuri.
Obţinem deci

Explicaţia acestui aparent paradox constă în aceea că nici unul dintre cele două “triunghiuri” dreptunghice , avand o cateta de 5 si cealaltă catetă 13 , nu este cu adevărat un triunghi deoarece ipotenuza este curbată (de fapt frântă), chiar dacă la prima vedere nu se poate afirma acest lucru.
Un triunghi având dimensiunile precizate, nu poate fi de fapt alcătuit din formele geometrice respective.
Ipotenuzele celor două triunghiuri mici (cel albastru şi cel roşu) nu au ambele aceeaşi înclinare. Cele două triunghiuri par a fi asemenea, dar dacă calculăm panta ipotenuzei triunghiului albastru obţinem: 5:2(=2.5:1) , în timp ce pentru triunghiul roşu raportul este 8:3(=2.(6):1) ceea ce demonstrează că ipotenuza triunghiului mare este de fapt o linie frântă.
Deoarece raporturile calculate sunt aproape egale, diferenţa este greu de sesizat cu ochiul liber cu atât mai mult cu cât marginile figurilor sunt destul de groase.
Dacă realizăm o imagine exactă a celor două triungiuri, eventual suprapuse, vom vedea că cele doua “ipotenuze” frânte formează un paralelogram al cărei arie este 1, adică exact diferenţa de arie dintre cele două triunghiuri.

Probleme distractive
- O populaţie de bacterii se dublează la fiecare oră a zilei şi se înjumătăţeşte la fiecare oră din noapte. Se consideră ziua de 13 ore şi noaptea de 11 ore. De câte ori va creşte populaţia de bacterii după 7 zile?
- O maşină pleacă la ora 12 din P cu viteza de 90 km/h. La ce oră îl va ajunge pe un biciclist plecat la ora 7 dimineaţa cu viteza de 15 km/h?
- O găină şi jumătate face un ou şi jumătate înt-o zi şi jumătate. Câte ouă fac 3 găini în 3 zile?
- De câte ori pe zi sunt limbile ceasului perpendiculare pe durata unei zile?
- Am tăiat o prăjitură în 4 părţi de-a lungul diagonalelor. Am mâncat o parte. Se cântăresc celelalte părţi şi rezultatele sunt: 120 g, 200 g şi 300 g. Care a fost greutatea părţii pe care am mâncat-o?
- Patru borcane cilindrice au fost dispuse pe fundul circular al unei cratiţe, cât mai aproape posibil, ca în desen. Dacă raza bazei unui borcan este 1, cât este raza bazei cratiţei?
- Două cercuri au centrle pe aceeaşi diagonală a unui pătrat. Ele sunt tangente între ele şi de asemenea, cu câte două laturi ale pătratului. Dacă lungimea laturii pătratului este de 1 cm, care este suma lungimilor razelor celor 2 cercuri?
- Formatul unei coli de hârtie numit A4, este un dreptunghi având raportul acelaşi cu raportul dreptunghiului obţinut prin tăierea colii A4 în două prin mijlocul lungimii. Să se calculeze .
- Intr-un depou se făcea manevra cu două locomotive; când acestea se aflau le distanţa de 30 m , pe aceeaşi linie ferată, mergând una spre alta cu viteza de 4,5 km/h fiecare, o muscă aflată pe tamponul din faţă al unei locomotive a pornit în zbor cu viteza de 6 km/h spre cealaltă locomotivă până la tamponul ei frontal, apoi imediat s-a întors la tamponul primei locomotive şi a tot făcut asemenea curse până când locomotivele atingându-se au strivit sărmana muscă… Ce distanţă a prcurs musca în această promenadă a ei?
- După 24 de ore populaţia de bacterii creşte de 4 ori deoarece se dublează pentru fiecare oră în plus dintre cele două cu care ziua este mai mare decât noaptea. După 7 zile populaţia se va mări de ori adică de ori.
- In cele 5 ore care s-au scurs de la ora 7 la ora 12, biciclistul a parcurs km. Peste încă o oră el va fi parcurs 90 de km, distanţă egală cu cea parcursă de maşină într-o singură oră. Deci după o oră de la pornirea automobilului, acesta se va afla lângă biciclist. Acest lucru se va petrece la ora 13.
- Există 3 mărimi: numărul de ouă, numărul de găini, şi numărul de zile. Prima mărime este direct proporţională atât cu a doua cât şi cu a treia. Aplicând de două ori regula de 3 simplă obţinem: O gaină şi jumătate face 3 ouă in 3 zile, în timp ce 3 găini vor face 6 ouă în 3 zile. Răspunsul corect este 6 ouă.
- De-a lungul unei ore oricare ar fi ea, minutarul este situat perpendicular faţă de orar de exact 2 ori. Cum într-o zi sunt 24 de ore, pe durata unei zile întregi, cele două ace ale ceasului vor fi perpendiculare de 48 de ori
- Considerăm numerele date ca fiind ariile părţilor de prăjitură. Astfel avem:
Obţinem deci
6. Unind centrele cercurilor mici se obţine pătrat cu latura , deci
diagonala este de , de unde diametrul cratiţei este . Rezultă că raza
cratiţei este de .Observaţie: Având în vedere caracterul distractiv al
problemelor/ întâlnirii nu s-a cerut demontrarea faptului că prin unirea
centrelor celor 4 cercuri obţinem un pătrat şi nici că centrul cercului
mare, centrul cercului mic şi punctul de tangenţă dintre cercul mic şi
cercul mare sunt coliniare pentru oricare dintre cercurile mici.
7. Distanţa de la centrul unui cerc la cel mai apropiat colţ este , respectiv . Diagonala pătratului mare se poate exprima astfel:
Cunoscând viteza de zbor a muştei, , distanţa totală pe care ar a prcurs-o în acea promenadă este:
7. Distanţa de la centrul unui cerc la cel mai apropiat colţ este , respectiv . Diagonala pătratului mare se poate exprima astfel:
- Mai întâi aflăm timpul necesar ca cele două locomotive să se întâlnească, ţinând cont că vitezele lor se adună atunci când se deplasează in sens contrar. Aceasta se va realiza împărţind distanţa la viteză:
Niciun comentariu:
Trimiteți un comentariu